티스토리 뷰
그래프 탐색 방법 중 대표적인 DFS와 BFS에 대해서 다뤄보려고한다
DFS와 BFS를 알기 전에
우선 이진 트리의 순회 방법에 대해서 짚고 넘어가자
트리에 있는 모든 노드를 한 번씩만 방문하는 방법인데
여기서 전위순회(Preorder Traversal) VLR방법이 DFS와 유사하다

현재 노드를 출력하고 왼쪽으로 쭉 갔다가
오른쪽이없으면 이전노드로 가서 오른쪽으로 가는 방법을 계속 방법한다

두 번째로 레벨순서 순회(Level-order Traversal)
레벨순서는 이진트리의 높이 순서대로 출력하는거다

루트노드인 +
그 다음 높은 *, E
다음으로 *, D
/, C
A B순서대로 출력한다
Level-order Traversal할때는 큐가 사용된다

처음에 루트노드인 +를 큐에 push 하고
반복문을 돌며
pop을 한번 해준다
그리고 ptr이 Null이면 탈출,
null이 아니면
출력하고
ptr의 자식노드들도 push 해준다
이런방식으로 계속 반복하면
레벨 순서에 맞게 출력이 된다
그래프의 DFS(Depth First Search) 깊이 우선 탐색
트리의 preorder traversal과 유사하지만
차이점은
그래프는 parent-child 구조가 아니며, edge 수에 제약이 없음
방문했는지(visitied) 기록해야한다, DFS는 유일하게 결정되지 않는다
구현 방법
1) iterative (stack + visit flag)
2) recursive (visit flag)
1) iterative
1. 시작 정점 V를 결정 : visit mark & push(v)
2. w= adjacent(top())
- 방문하지 않은 정점 w 존재 : push(w) & visiting mark
- 방문하지 않은 w가 없음 : pop()
3. goto 2, 스택이 공백이 될 때 까지 수행
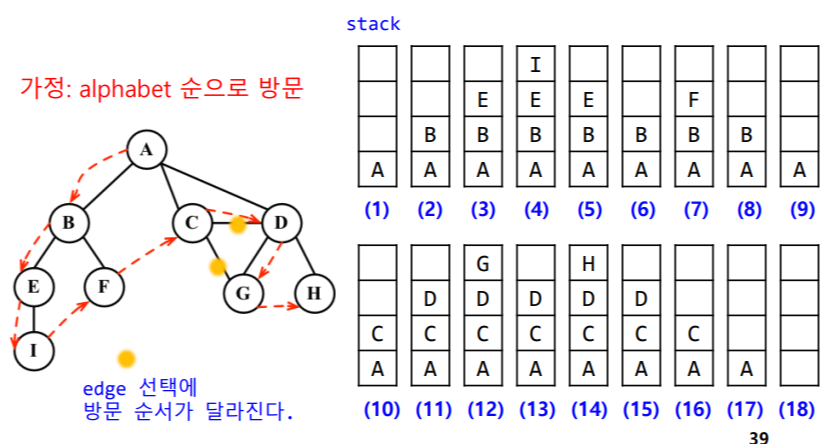
가정 : alphabet 순으로 방문
1) A push & visit mark
2) B 방문
3) B push & visit mark
4) E 방문
5) E push & visit mark
6) I 방문
7) I push & visit mark
8) I에서 방문하지 않은 w가 없음
9) I pop
10) E에서 방문하지 않은 w가 없음
11) E pop
12) B에서 방문하지 않은 w가 있음
13) F 방문
14) F push & visit mark
.
.
.
대충 이런식으로 하면 DFS 결과가
A -> B -> E -> I -> F -> C -> D -> G -> H
1 -> 2 -> 5 -> 9 -> 6 -> 3 -> 4 -> 7 -> 8
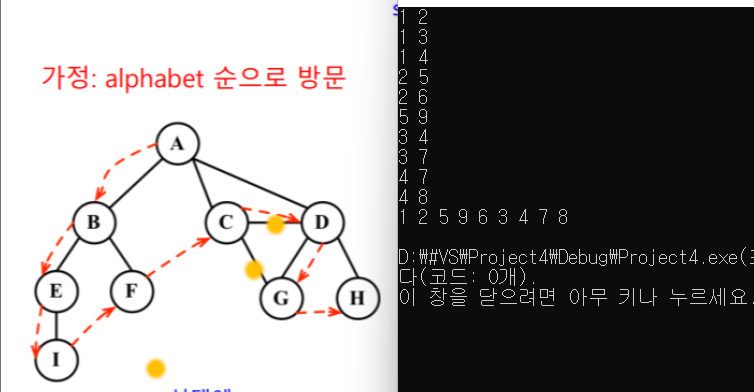
stack을 이용한 DFS iterative 코드
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>
#define MAX 1001
using namespace std;
bool visited[MAX];
stack<int> s;
void initialize(int N) {
for (int i = 1; i <= N; i++) {
visited[i] = false;
}
}
void dfs(vector<int> v[], int V) {
s.push(V);
visited[V] = true;
cout << V << " ";
int current,next;
while (!s.empty()) {
bool visitcheck = false;
current = s.top();
for (int i = 0; i < v[current].size(); i++) {
next = v[current][i];
if (!visited[next]) {
s.push(next);
cout << next << " ";
visited[next] = true;
visitcheck = true;
break;
}
}
if (!visitcheck) {
s.pop();
}
}
cout << "\n";
}
int main() {
int N, M, V;
cin >> N >> M >> V;
vector<int>* graph=new vector<int>[N+1];
//vector<int>graph[n+1]
//vector<vector<int>> graph(N + 1);
for (int i = 0; i < M; i++) {
int a, b;
cin >> a >> b;
graph[a].push_back(b);
graph[b].push_back(a);
}
for (int i = 1; i <= N; i++) {
sort(graph[i].begin(), graph[i].end());
}
initialize(N);
dfs(graph, V);
return 0;
}current는 현재 탐색하는 vertex고
next는 current와 연결된 vertex들을 차례대로 찾는 것이다
next중에 visit이 다 됐으면 pop을 해주고 current가 바뀌고
next중에 visit된애가 없으면 새로 push 해주어서
얘가 다음 current가 되어 또 탐색을 한다
2) recursive

보통 c++로 recursive로 구현한다고하면
저기 저 오른쪽위에 인접리스트를 벡터라고 보면된다
예를 들어 정점이 0,1,2,3,4,5,6,7이 있으면 6같은경우 2와 7과 연결된것이다
그러면 현재 w가 6일때 2로 이동하고 2는 또 0으로 이동하고 0은 또 어디로 이동하고
이렇게 연결된 vertex로 재귀적으로 dfs를 수행하도록 하고,
방문한 vertex는 visit표시를 해놓는 것이다
DFS recursive
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#define MAX 1001
using namespace std;
bool visited[MAX];
void initialize(int n) {
for (int i = 1; i <= n; i++) {
visited[i] = false;
}
}
void dfs(int current, vector<int> graph[]) {
bool check = false;
for (int i = 0; i < graph[current].size(); i++) {
int next = graph[current][i];
if (!visited[next]) { //방문안했으면
visited[next] = true;
cout << next << " ";
dfs(next, graph);
check = true;
}
}
if (!check)
return;
}
int main() {
int N, M, V;
cin >> N >> M >> V;
vector<int>* graph = new vector<int>[N + 1];
for (int i = 0; i < M; i++) {
int a, b;
cin >> a >> b;
graph[a].push_back(b);
graph[b].push_back(a);
}
for (int i = 1; i <= N; i++) {
sort(graph[i].begin(), graph[i].end());
}
initialize(N);
visited[V] = true;
cout << V << " ";
dfs(V, graph);
cout << "\n";
return 0;
}
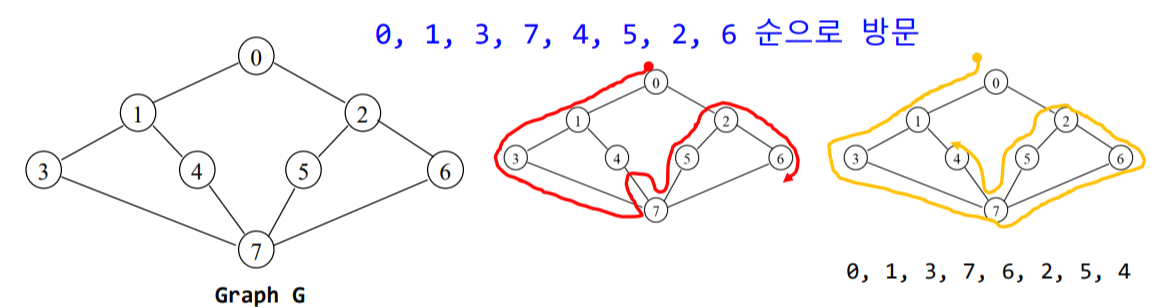

한 예시를 더 들어보면
0에서 DFS를 시작하면
작은 순서로 1을 방문하고
0 -> 1
1은 3과 4중에 작은 3을방문하고
0 -> 1 -> 3
7을방문하고
0 -> 1 -> 3 -> 7
7은 4와 5중에 4를 먼저가고
0 -> 1 -> 3 -> 7 -> 4
5를가고
0 -> 1 -> 3 -> 7 -> 4 -> 5
2를가고 6을간다
0 -> 1 -> 3 -> 7 -> 4 -> 5 -> 2 -> 6
너비 우선 탐색(Breath First Search)
1) iterative ( queue + visit flag)
2) recursive (visit flag)
1) iterative ( queue + visit flag)
1. 시작 정점 v를 방문
visit marking & enqueue()
2.w=dequeue()
visit marking & 방문하지 않은 w의 인접노드 enqueue()
3. goto 2, queue가 empty 일 때 종료
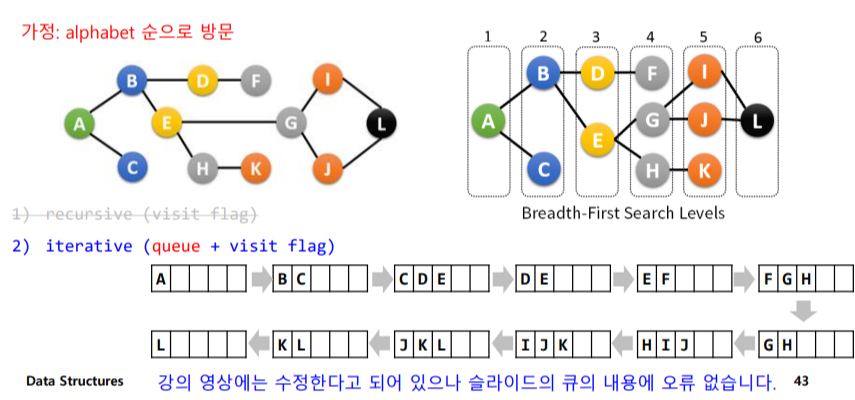
A부터 시작하면
1) A visit mark & push
2) A pop
3) A 인접노드 B,C push
4) B visit mark & pop
5) B 인접노드 D,E push
대충 이런식으로하면
A -> B -> C -> D ->E -> F -> G -> H -> I -> J -> K -> L 순대로 방문한다
#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>
#include <queue>
#define MAX 1001
using namespace std;
stack<int> s;
queue<int> q;
bool visited[MAX];
void initialize(int N) {
for (int i = 0; i <= N; i++) {
visited[i] = false;
}
}
void bfs(vector<int> graph[], int start) {
visited[start] = true;
q.push(start);
int current, next;
while (!q.empty()) {
current = q.front();
q.pop();
cout << current << " ";
for (int i = 0; i < graph[current].size(); i++) {
next = graph[current][i];
if (!visited[next]) {
q.push(next);
visited[next] = true;
}
}
}
cout << "\n";
}
int main() {
int N, M, V;
cin >> N >> M >> V;
vector<int>* graph = new vector<int>[N + 1];
for (int i = 0; i < M; i++) {
int a, b;
cin >> a >> b;
graph[a].push_back(b);
graph[b].push_back(a);
}
for (int i = 1; i <= N; i++) {
sort(graph[i].begin(), graph[i].end());
}
initialize(N);
bfs(graph, V);
return 0;
}
2) recursive (visit flag)
recursive는 강의자료에 없어서 패스
'개념' 카테고리의 다른 글
| git 이전 커밋 수정 (0) | 2023.01.04 |
|---|---|
| git merge conflict 해결 (0) | 2022.03.21 |
| 노트북 부품 및 운영체제에대한 개념 (0) | 2022.02.24 |
| 네이티브 앱 vs 하이브리드 앱 vs 크로스 플랫폼 앱 (0) | 2022.02.16 |
| 와이파이 비밀번호를 알아내는 방법 (0) | 2022.02.06 |
- Total
- Today
- Yesterday
- 데이터3법
- html
- 데이터베이스
- SpringBoot
- 2024인프콘
- Android Studio
- 리눅스
- 우분투
- 클로아
- infcon 2024
- 인프콘2024
- authorization_code
- 오픈소스
- SQL
- authorization code
- html #웹 #웹사이트 #플레이리스트
- 데이터 3법
- 로스트아크 캐릭터
- 프로그래머스
- git 예전 커밋 수정
- DDL
- oauth
- DML
- javascript
- kloa
- git
- oauth2.0
- CSS
- git commit 수정
- bfs
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
